La marelle est un jeu dont on ne connait pas précisément les origines. On en retrouve toutefois les traces sur certains sites archéologiques ainsi que dans des textes qui nous sont parvenus (Ovide). Le jeu est relativement simple, et existe sous différentes formes. La version que je présente ici est une version à neuf cases.
On trouve cette version sous le nom de « marelle romaine » auprès de créateurs de jeux historiques ou médiévaux. Elle a la particularité d’avoir un point central, présent à l’intersection de quatres lignes de jeu.
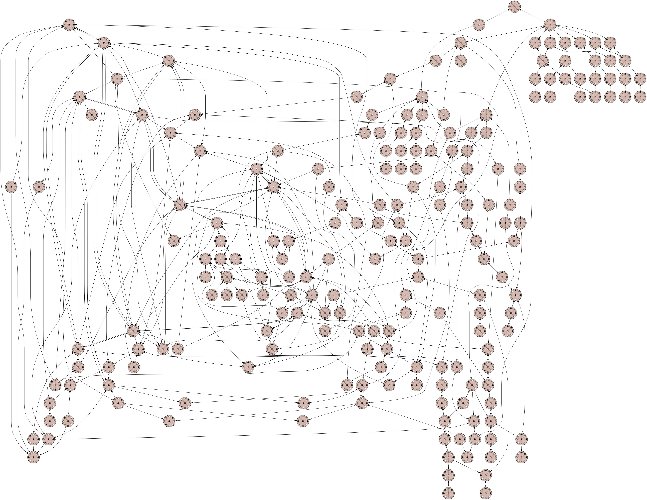
D’autres sites se sont déjà intéréssés au rapport entre mathématiques et le jeu de marelle et je ne vais pas chercher à les reprendre ici. Par contre, j’ai essayé de tracer l’ensemble des parties possibles dans un graphe en fonction des différentes actions des joueurs (en partant du principe qu’un joueur n’irait jamais jouer un coup qui lui est directement défavorable). Un extrait du graphique final est présenté ci contre, et le résultat peut être visualisé en ligne.
Cliquez sur l’image pour la voir en taille réelle :
A strange game. The only winning move is not to play
Chaque dessin représente un plateau, avec ses pions blancs et noirs. Les lignes permettent de suivre les coups des joueurs et d’aller à une configuration à une autre ; la couleur dans le cercle indique quel est le joueur qui vient de jouer. Le jeu commence par un plateau vide (tout en haut de l’image), et est rempli au fûr et à mesure par les joueurs. Une fois que les joueurs ont posé leurs pions, ceux-ci sont déplacés sur le plateau, selon les règles que nous connaissons aujourd’hui.
Par soucis de lisibilité, j’ai retiré les jeux suicidaires où ceux qui conduisent à des coups inutiles, je n’ai conservé que les cas où les joueurs essaient d’améliorer leur configuration sans pour autant pousser la réflection trop loin, car le jeu devient entre alors dans une partie infinie. D’autre part, les différentes symétries par rotation ne sont pas représentées, afin de ne pas surcharger le graphique.
Au final, le jeu ne présente pas trop de surprise, les deux joueurs peuvent jouer indéfiniment s’ils ne font pas d’erreur ; la moindre erreur signifie souvent la fin de la partie si l’adversaire est attentif. Je ne m’attendais toutefois pas à autant d’étapes et de configurations différentes dans le jeu !
Technique
Le calcul des combinaisons et des différents coups est réalisé en scala, chaque plateau est une scène povray, et graphviz a servi à calculer le graphe. L’ensemble du code est disponible sur mon dépôt git.
Attention à la mémoire disponible si vous souhaitez recréer le graphique, dot est très gourmand er RAM dès qu’il s’agit de grandes surfaces à calculer…